Reflexions about volatility

Investing / Others
1

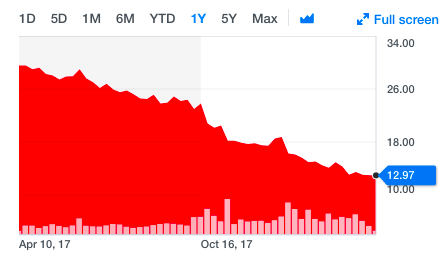
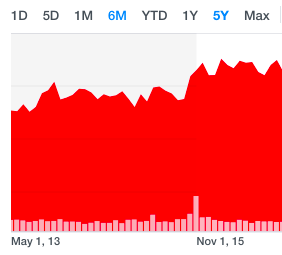
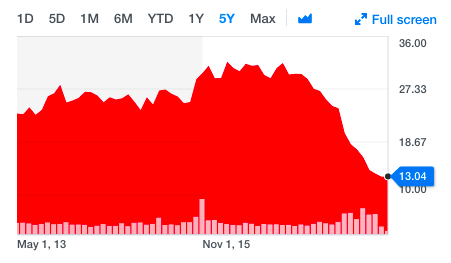
Or even less! Sometimes you can acquire companies for less than (cash - total debt), i.e liquidation value. See my thread on Net net stocks as an example.

That is also something about modern finance that I could never had a grasp on. Why do they tell us that volatility = risk as a perfect equivalence?

  • I understand this in the context of a short period of time. Let’s say that you invest 1000 CHF today, in a quite fairly priced company stock. Because the price fluctuates around the fair value, you do not know if, for instance, in a week you will still have 1000 CHF. You may have more, you may have less. But so far it is just in accordance with the accounting principle of matching your assets with your liabilities : don’t invest in long term assets if you want the money back next week because you need it.

  • Now for risk vs volatility in itself. I think we can admit that risk is a definitive impairment of invested capital. Let’s see how volatility fits in this. Let’s compare the price action of stock of two companies :

  1. The stock of company A goes up 10%, then up 5%, then up 15%. The total return is 32%, and the standard deviation is 5.
  2. The stock of company B goes down 15%, then down 15%, and down 15% once again. That is a cumulated loss of 38%.
    The volatility and standard deviation are zero!

Modern theory tells you that stock B is less riskier than stock A. In fact it tells you that it is almost risk free because volatility is zero! But of course your wallet says otherwise.

Warren Buffett has also a point when he explains his acquisition of the Washington Post :

He related the story of his acquisition of nearly 10 percent of the Washington Post Company for $80 million in 1974. According to Buffett, the entire company could easily have been sold for $400 million at the time and no expert would have questioned this valuation.
“Now, under the whole theory of beta and modern portfolio theory,” Buffett said, “we would have been doing something riskier buying the stock for $40 million than we were buying it for $80 million, even though it’s worth $400 million – because it would have had more volatility. With that, they’ve lost me.”
Buffett’s investment grew 25-fold over the next 15 years.

And finally, I have never seen an investor complaining that his stock is volatile on the way up. Only on the way down.

Sorry if I argue a lot with you but I do this for several reasons :

  1. You seem to be willing to learn
  2. I see that a lot of newcomers on the forum are drinking modern finance theory academia like gospel. Be wary that not everything that modern finance says is relevant. This is especially confusing because many of the evangelists of modern finance got a nobel for their work (Markowitz, Fama, Merton and Scholes,…). People at the time were happy to finally be able to put equations on finance and make it mathematically tractable. But as the old saying goes, “better be approximately right than precisely wrong”.

To come back to the initial topic :

  • small caps are interesting because no institutional investor goes there, making the market a lot less efficient
  • value stocks are interesting because as said earlier, it allows you to buy a dollar for 50 cents.

In my portfolio i invest exactly in small caps value stocks. But not with ETFs, and especially not with multifactor ETFs, for the reasons mentionned above.

1 Like
2

It is at least the theory behind multifactor investing. It was initiated by Eugene Fama, the father of the Efficient Market Hypothesis. Several years after having formulated the EMH (and that the EMH was by then vastly taught in academia), Fama noticed that two sub-sets of the stock markets consistently beat the market : small caps, and value stocks.

Instead of just admitting that the EMH does not always work everywhere all the time, Fama concluded that, since these stocks consistently bring better returns, they must be riskier. As you can tell by now, I think this is nonsense, formulated by a guy who could have the heart to deny his cherished theory.

It is indeed nice, we can see how central banks policies progressively deteriorates the returns of asset classes.

Volatility, standard deviation and variance all refer to the same thing, with variance = (standard deviation)^2
However, as i said in my previous post, I strongly disagree with it being a good proxy for risk. Risk is permanent loss of capital, not the volatility of a stock.

3

I’d say that risk is highly subjective, but for most people potential loss of their portfolio value by, let’s say, 25% in short time is a significant risk and the easiest way to estimate such possibility is to measure volatility.

I think you’re oversimplifying a lot in your critique of financial economics. People in academia clearly know that upward volatility doesn’t constitute risk. The usage of volatility is about mathematical modeling and quantitive measurement of risk.

Nobel laureates in economics might be overusing math and statistics to describe reality, but they are not dumb.

1 Like
4

I agree with that. That will make a common ground for further discussion :slight_smile:

Let’s say that we have found a measure if the riskiness of a stock. Then I would expect that:

  1. If a stock is risky, the risk measure should give us a good hint about it.
  2. The riskier a stock is, the stronger we should receive a hint from the measure.

Do we agree on this as well?

If that is the case, then I have trouble understanding how volatility follows these principles.
To begin with, let’s agree on the volatility definition : in academia, volatility is not the volatility of a price per se but it is defined as the standard deviation of daily returns. And this is not the same thing!

Why, you may ask. If we take back your example of a -25% drawdown, we could expect the price of this stock to be fairly volatile. But when we consider daily returns, it is perfectly possible to have very low volatility and large drawdowns.

Let’s take two examples, one theoretical, and afterward one from a real company.

  1. Imagine a stock whose price would start at 100 and then would realize, each day, a loss of exactly 0.95%. So each day, the daily return is 0.9905, and we let it compounding. After 30 days, it would have realized a total loss of 25%. Which is, according to what we said earlier, quite risky! But when we look at the standard deviation of daily returns, since these returns are constant, the volatility is absolutely null.

So we are in a situation where this hypothetical stock would lose steadily value day after day, almost as a straight line, but where the volatility measure would tell us that this stock is not risky.

Of course, I hear some of you say that such a use-case is irrealistic; in the real life, prices fluctuates much more than that. So at least there would be some noise in the daily returns of the stock! The volatility would then surely show a more accurate picture of the risk.

Or does it?

  1. Let us take as a real example the following company :
    GE

This is the performance for last year of a “blue chip with diversified sources of income”. It is none other than General Electric! In term of blue chip with diversification, this is quite the stereotype.
I think we can agree than last year, the stock has been a nightmare for its shareholders : the losses amount to around -55% for the year. Which I won’t deny is quite risky.

However, the performance of the daily returns look quite steady as well… there is a little bit of noise, but the chart is almost a straight line and, although i did not calculate it, I would not be surprised if the volatility over the period is quite low.

So that is my first big pain point with volatility : how come that for a stock that has been as risky as GE, the official measure of “riskiness” does not paint an accurate picture of the risk?

Now let’s push the investigation further: the beta of GE is 0,71. So officially, it should mean that GE is less less riskier than the market! If i understand it correctly, it should mean that the stock has less volatilty than the market and, when the market goes up, the stock goes a little bit less up, but when the market goes down, the stock goes a little bit less down.
So now we have last year, where the US market had a record low volatility, and superb profits of 20+% for the year, and on the other hand, GE, a less volatile stock but that managed to lose 55% over the year. I may have even more pain points having a firm grasp on the notion of beta.

But let’s go back to volatility : Let’s look at GE stock before 2017:
GE2

The stock is a little bit more volatile but still look steady, with a clear trend on steady gains. So the volatility may be higher, but nothing that would make us expect a 55% drawdown in a year.

Now let’s look at the full picture:
GE3

Here we can say that finally the stock has been quite volatile AND risky. But it also raises a lot of questions :

  • it looks like the volatility depends a lot on the observed period, which may be fine if it was stationary and converge on the long term
  • However, I really doubt that the vol is stationary (but if someone is willing to prove me wrong, I’ll happily accept my mistake). So for instance, an investor at the eve of december 31st, 2016, would have looked at GE volatility and would have concluded that this measure of risk tells that the stock is not very risky. His wallet would have strongly disagreed.
  • and finally, and perhaps my biggest interrogation : if volatility is not stationary and does not converge, then past volatility does not tell us anything about future volatility. How then, by looking at the current volatility of stocks, can we then say that such and such is risky, but that so and so is not? And most importantly, if we need to know the future volatility of a stock (which is quite challenging), of what use is it to assess its current riskiness?

Sorry if I sounded arrogant in my posts. I gladly accept that Nobel laureates are far from dumb.
On the other side, this community is all about taking responsibility and ownership of our life and what we do, and thus i would guess that it is important that we understand as much as possible what we are doing.
And that is what I am trying to do : even if volatility is one of the biggest pillars of academics finance, I try to understand what it means. If someone has valid answers for my pain points, I will gladly accept them. But I have to concede that so far, when people say as a gospel “High(er) Vol = High risk, Low(er) Vol = Low Risk”, I am quite puzzled. Looks like volatility is much more uncorrelated to risk that seems at first sight.

1 Like
5

There ąre different kinds of risks in the stock market. It’s nothing new under the Sun. Volatility doesn’t measure the direction of price movements, but just dispersion. Of course, the direction is probably more important than dispersion, but this doesn’t make the dispersion measurement useless. It does matter for most of the people, not only whether their investment goes up or down long-term, but also whether it jumps from +95% to -95% a day. Maybe for you such jumps aren’t a risk, but for me they are.

Most people are expecting not only positive returns (long-term upward trend), but also risk-adjusted positive returns and high volatility is one of the major negative characteristics (you don’t have to call it “risk” if you want) that people don’t want. There are of course other measures of risks: alpha, beta, R-squared, standard deviation or Sharpe ratio. There are probably also risks that are difficult to measure (risk of drawdown, risk of bankruptcy due to some unexpected event, etc.). Still, none of these characteristics make volatility useless for an average investor.

It’s just important to remember that volatility is not the only risk in the stock market and I think there’s no controversy in academia about it.