Your portfolio is (probably) not efficient

Investing / Portfolios
1

I want to have a rational asset allocation so I did a bit of reading about modern portfolio theory.
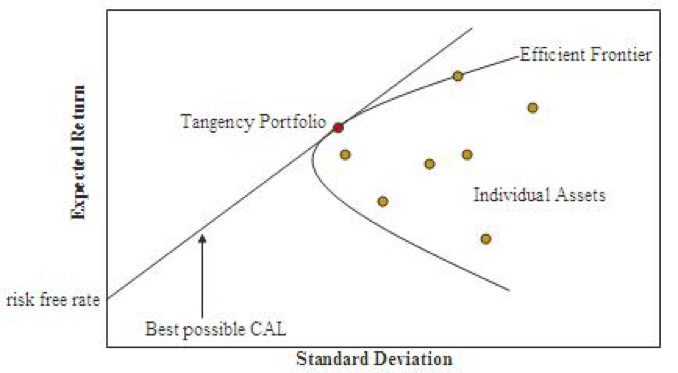
There is this nice idea of plotting all the risky assets on two axis: risk vs. return
image
Then for each fixed level of return, you can find the unique combination of assets that minimizes the risk. That defines a point for each return levels, and gathering all these points you get an “efficient frontier”, where all the “good” portfolios are. You want your portfolio to be on this frontier if you’re a rational investor.

A further claim is that the Total Stock Market portfolio (like VT) lies on the efficient frontier. That means that if you only have VT in your portfolio, it’s a bit boring, but also maximally efficient. So you should give your own shoulder a deserving pat.

But this last point is actually very wrong.
Let me explain: a portfolio on the efficient frontier is defined by the weights that are associated to each asset, and the only constraint on these weights is that they have to sum up to 1.

Since these weights are somewhat random numbers only constrained by “sum = 1”, one would assume that some of these weights can be negative.
In Impossible Frontiers, two finance professors show that indeed as soon as you have more than > 100 assets to pick from it becomes extremely likely that some of the weights are negative numbers, and that this is the case for all the portfolios on the efficient frontier.

But, by definition the Total Stock Market portfolio has positive weights on every assets. So it does not lie on the efficient frontier. And as long as your portfolio in not shorting at least one stock, it also cannot be on the efficient frontier.

So none of our portfolios are efficient. I find this thought very liberating :slight_smile:

2 Likes
2

Take what you read online about MPT with a grain of salt until you have played with it yourself.

It’s a cute theoretical tool and teaches a few important lessons about diversification, but is not particularly useful for practical portfolio optimization at least in the form that’s commonly taught.

It requires you to have the clairvoyance of knowing expected future returns and correlations between assets. And it’s quite sensitive to small perturbations in these inputs - small changes may produce very different output recommendations from the optimizer. So there’s no the efficient frontier, it’s only as good as the inputs you feed into the model - which you’d normally fit from historical data but correlations may change overnight especially during crisis.

By whose definition? And where did such huge assets classes as debt, commodities and real estate go?

3 Likes
3

Knowing that MPT is okay to explain diversification but doesn’t travel much further like @kilyn said, the more accurate claim would be to say that the “market porfolio” lies on the efficient frontier. This theoretical market portfolio contains the whole market, not just the shares on VT since other assets (and asset classes!) are not taken into account.

1 Like
4

Thanks @Ed_Waadt and @kilyn for correcting me. In the paper Impossible Frontier the authors indeed talk about the “market portfolio” (the portfolio of all assets in which each asset’s weight is proportional to its total market capitalization).

If you believe the conclusion of that paper, then the “market portfolio” cannot be on the efficient frontier as it’s not shorting any asset and all the portfolios on the efficient frontier must be shorting at least one asset.

As @kilyn said the real efficient frontier is essentially unknowable. Furthermore, even if an oracle were to tell us the correct expected returns and covariances, the frontier moves every day.
So holding a portfolio on it would never be cost-effective.

6

In the paper I mentioned, having a negative weight for one asset simply means taking a short position on that asset. The authors give an example on page 8 after Proposition 2: with only 3 assets you can already build cases where portfolios on the efficient frontiers have negative weights. (This other paper has a similar example).

In their analysis the authors of the first paper show that as the number of assets increases, all the portfolios on the efficient frontier are going to have at least one negatively weighted asset. Hence the market portfolio cannot lie on the efficient frontier (because as you said that portfolio cannot have negative weights).

The paper aims at disproving that the market portfolio is efficient. It’s a critic of that conclusion of a strong version of the efficient market hypothesis.

Does this amount to the same as doing factor investing, e.g., small cap (VBR)? When you leverage your portfolio you increase both the return and the volatility If, as you mentioned, you manage to get a risk-free loan with no interest, both return and volatility are simply multiplied by your leverage. If you invest in small cap, you also in effect increase both return and volatility. Is there a difference (aside from comparing the sharpe ratios)?

9

Can you explain further what you mean by “self funded leverage”?

Would you like to explain where your >10% come from?

Regards,

Another Tea Lover

11

I agree with you on this premise.

Agree

I partially disagree. I would say that one component of your risk tolerance is always bound with your current life situation. I would say to discuss that further we somehow need a mutual definition of risk.

That is one of the reason I am trying to get my investment approach straight in my mid twenties.

Agree

Agree, but keep in mind that the future is uncertain. Your discounted life-time-income in t=0 doesn’t have to be the same as your realised life-time-income in t=100.

Don’t agree on this point, but it really depends on your risk definition.

Your explanation makes sense, but it seems to have a lot of assumptions which aren’t that obvious for me.

In what kind of tea are you into?

Kind regards,

Another Tea Lover

2 Likes
12

Very interesting read, thanks! I hope you’ve had your sip of tea, @TeaCup, because self leverage is a topic I’m very willing to explore.

A limitation to leveraging from day one that you didn’t mention is access to capital. As a young person with what I think a stable job and a high risk tolerance, I am actively searching for ways to get leverage to invest. I may not have explored every option but that seems pretty difficult in Switzerland.

At day one, you can’t get a lombard loan because you have no assets to back it. You can’t get a mortgage because you likely don’t own a house yet. All the other commercial kinds of loans I’ve found require heavy amortization that makes it unsustainable to hope to get good returns by investing them. That leaves friends and family loans, which bear another kind of risk in that they can put a strain on your relationships (we’re back in risk tolerance territory, though).

That makes leveraging yourself from the onset unsustainable as a swiss resident, I feel, but I’ll gladly take all suggestions as to where to find credit where the cost of credit doesn’t cancel the benefits from it.

As your wealth grows, then you can start to access lombard loans and mortgages that allow you to get leveraged but as your wealth grows and you get older, the total mass of your future savings diminishes, as well as the total expected returns on the amount you can invest, making it less relevant to get leverage as opposed to right at the start of your investment journey.

There’s probably a period of time during which it would make sense to get whatever leverage you can when you can start to access it but by the time you reach it, forces of habits are likely to have set in and you’re also likely to rationalize why it’s not worth it going into leverage anymore.

I may be wrong but I’d say that the limits we put on access to credit, which are a good thing to prevent careless people to get into unsustainable debt, play a big role in why not more people go into leveraging themselves and investing according to their risk tolerance from the start. Have I forgotten to take a source of credit into account?

Edit: Aaaand… a quick trip in the “Should I buy TSLA shares” thread reminded me that I have forgotten to take leveraged ETFs into account. I’ll have to study that, though they bear yet a different kind of risk (namely, for me, investing in foreign assets subject to financial/taxation treaties fluctuation - I haven’t been able to find a leveraged swiss ETF investing in swiss assets but there again, I may not have searched deeply enough).

3 Likes
13

Have you looked at “Lifecyle Investing”? It’s a book about implementing that strategy (time diversification via leveraging heavily when young). Famously, the user “markettimer” on boglehead tried that approach in 2007 (It didn’t work out).

If you don’t want to take a loan, you can in effect have a leveraged position via futures contracts or options. That’s what the authors of Lifecycle Investing describe in chapter 1 (The implied interest rate for these contracts is usually lower than IB margin loan rate)

leap_of_faith
leap_of_faith494×510 56.6 KB

2 Likes
14

He didn’t try that approach exactly, he had much more leverage and increased it through the dips instead of resetting the leverage as the strategy advises.

1 Like
15

Basic derivatives come always with a lever of at-least 10. But keep in mind a lever works in both directions…

Not true. SQ offers me already lombard loans and i have atm less than 10k invested.

Regards,

Another Tea Lover

1 Like
16

Gonna check that out. Thx

17

I must admit I haven’t read the book. I have read market timer’s thread and he did it using 0% credit card opportunities (at first, then high interest credit cards because it is a slippery slope) and derivatives. We don’t have credit card offers that would offer significant leverage. Derivatives are complex tools that I don’t pretend to understand (I’d have to study it but won’t set the required time aside just now due to other priorities). It feels to me like they’re adding yet another layer of risk by not representing a tangible asset, being just a contract instead. How would this additional risk enter the calculation of risk-adjusted returns smoothed on a lifetime?

Sure, that’s the risk part of the equation, which must be accounted for in the need, ability and willingness to take risk, considered on a lifetime basis. I wouldn’t take on leverage now, when times are quite uncertain.

Thanks for the clue. I haven’t been able to find it on their website so what are their margin requirements (how much are they willing to loan you for 10k invested and what would trigger a margin call)?

As a whole, I think that not all debt is created equal and that it translates in the ability and willingness we have to take risk. A young person with good human capital but low wealth may have high need to take risk. She may not have much to loose, so a good ability and willingness too but risking family relationships (family loan) isn’t the same as risking bankruptcy which, in turn, is not the same either as risking loosing whatever amount of money we have invested… As well, I may have the ability to take on more fiscal risk with more wealth, because I can hire an attorney, but have a much lower ability to take that kind of risk at the start of my journey.

I’m comfortable with the risk of my investments loosing value (or even going to zero). I’m not sure it’s quite the same as being willing to risk bankruptcy (taking on loans), the ability to travel aborad (investing in foreign assets I don’t know enough that may carry legal consequences in the long run) or mortgaging relationships. Which basically means that I’m not that big a believer in life cycle investing, unless one can access cheap low risk loans, which should be very hard to find because someone with the ability to loan you money to invest at a profit with low risk on the loan should be able to secure a better return for himself by investing it himself.

The bottom line of my thinking? The credit market is efficient and it’s very hard to find a truly interesting loan on a risk adjusted basis.

19

Despite what I probably sound like, I basically get to the same point from the other side of the train thought. There’s a world of difference between the thought exercise of borrowing future money to invest it now and actually doing it: the people lending you that money are doing it to get their own profit. To them, you are the risk. They want to be compensated for it.

On a risk adjusted basis, getting a loan should not be more efficient than investing your own money (and since the other party is likely to have more time, skill and means than us when making a loan contract, they’re likely to have more ability to pull things at their advantage, so us to end up with the short end of the deal).

20

The story has a happy ending: 13 years later markettimer is now thinking to retire with 1.5M.
Of course, there is more to that story than lifecycle investing and I would not want to try myself that kind of extreme leverage, but I think one conclusion is that young people have the capacity to recover from liquidation of their portfolio (as the present value of their future earnings is still in the millions).

(Fun aside: Jack Bogle recommending young investors to leverage 2:1 at 5:40)

21

No clue if you call it a margin call with lombard loans (what I know for sure is that you call it a margin call with futures), but they are willing to grant me a loan of 46% of my invested value.

Keep in mind that with a loan you can go below zero. That is the reason I am very interested in @TeaCup risk definition.

I would say the credit market is even less efficient than the stock market, but that is another discussion.

1 Like
22

Totally agree

Can you recommend a paper on that topic?

Ohh I am not that much into black tea, it doesn`t let me sleep at night…

Regards,

23

If you know where I can find someone that bails me out at the bottom and Iet me pay back later you will get a commission :wink:

24

How deep is the bottom?

25

That was a Joke :wink:

A fast calculation:

Life-time-income: 2 Mio. CHF
Lever: 3
Black Thursday: -90% on the DOW

(2 Mio. CHF x 3 X 0.1) - 4 Mio. = - 3.4 Mio.