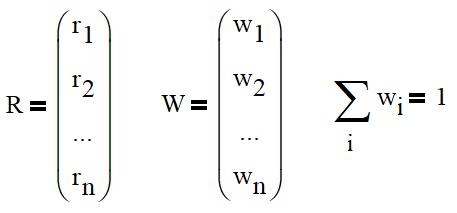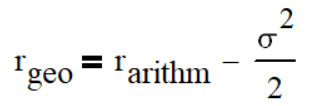So, now let’s say we have a portfolio containing certain assets 1,2,…,n and we try to maximize our future profit by maximizing expected geometric return via a proper allocation of these assets with weights w1, w2, … wn (sum is 1). Weights can be also negative, meaning we are short-selling an asset or borrow cash.
How can we do this?
We can find a theoretical answer with a help of so called “Modern portfolio theory”. General Wikipedia have a very comprehensive description
We have to calculate two things: an expected (arithmetic) return rate r1, r2, … rn and a covariance matrix Σ. Covariance of two distributions in statistics is the expected value (mean) of the product of their deviations from their individual expected values.
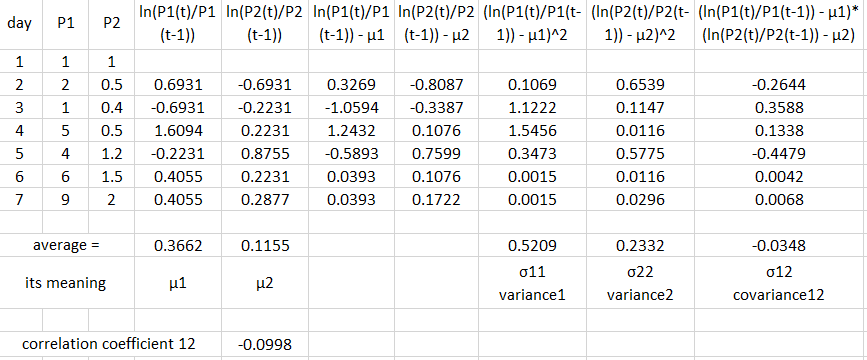
Let’s say we have historical data for two assets P1(t) and P2(t). Here is a small example how we would calculate (historical) return rates and covariance between these two assets:
First we need price data for 2 assets (P1 and P2). Each row corresponds to values of P1 and P2 at the same moment, e.g. closing prices/NAV in the same day. Then we calculate ln(return ratio), here after one day, for both prices. The average of values in individual rows is the mean of lognormal distribution of return ratios μ1,2. As a next step, we need to calculate a deviation of individual ln(return ratio) from its mean value, (ln(return ratio)-μ). If we now square these deviations and calculate average value of the results, we obtain the variance of returns for respective assets. But if we multiply deviations for different assets and calculate average of the results, we obtain a covariance of returns for assets 1 and 2. In this case it is negative, meaning that on average prices of 1 and 2 go into opposite directions.
Note that one should probably annualize mean return and mean co/variances by multiplying obtained values by a number of periods corresponding to a full year, and calculate an arithmetic annual return rate r = exp(μ)-1.
While co/variances is all we actually need, it is interesting to look at a correlation coefficient for two assets. It is given by
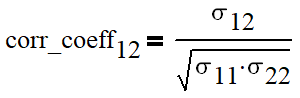
The value of the correlation coefficient is limited and lies between -1 and 1. It is 1 if asset changes are always go in one direction, 0 if changes are completely independent and -1 if they always go in opposite directions. In this case the value of the correlation coefficient between 1 and 2 is slightly negative, meaning that in average the prices of two assets change rather in opposite than in the same direction.
Back to the covariance matrix Σ: for assets 1,2,…n, the element of the covariance matrix Σ(i,j), 1 ≤ i,j ≤ n, is equal to the covariance of assets i and j. Every diagonal element (i=j) is a covariance of the asset i with itself, that means, variance.
The expected (arithmetic) return of the portfolio and its variance is best calculated using vectors and matrices. Let R and W be vectors containing annualized expected returns and weights of respective assets in the portfolio:
The covariance matrix contains annualized co/variances calculated as outlined above.
The expected (arithmetic) return of the whole portfolio is then simply a weighted average return of all assets:
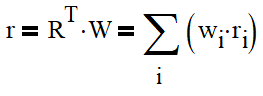
The variance of the whole portfolio is given by the following formula:
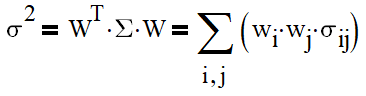
Finally, our tasks consists of finding weights of assets that maximize the geometric return of the whole portfolio:
And that was a general theoretical description of a multi-asset portfolio.
As always, looking forward to your feedback!
(to be continued)