tl;dr: Options are complex instruments, but can be a useful way for a Swiss investor to get margin capital, because there are problems with leverage, withholding taxes and debt interest.
Incorporate
tl;dr: If you want to leverage, incorporation is not that bad.
Why would that be important? As a natural person leverage is not easy in Switzerland. There seem to be forum members which use leveraged ETFs without being classified as professional securities trader. But legal certainty is low and the more complex and custom the strategy the more uncertain.
So what about removing that problem by incorporating a limited liability company?
- Sure, you pay taxes on everything (including capital gain), but taxes are as low as 12% in Switzerland.
- Sure, you can’t book holidays with this money, without first paying tax on dividends, but it is reduced by a lot. The total is likely lower than being taxed as a professional securities trader
- Also you stop paying high taxes on everything and only pay fully on consumption.
- You can deduct losses up to 7 years and you can defer paying taxes on capital gains by not selling.
- Live in Zurich but pay (company) taxes elsewhere.
Withholding Tax Problems
tl;dr: Debt interest is bad in combination with withholding taxes.
The updated ordinance on deducting foreign withholding taxes “Verordnung über die Anrechnung ausländischer Quellensteuern” (German) in force since 2020-01-01 reduces the deduction for companies by debt interest paid (art. 10-11) . It is rather complicated how they attribute it to your asset positions. But it will in essence have unrecoverable withholding taxes fully apply on a significant part of the gains you didn’t really have (because you needed to pay debt interest with those gains). Since dept interest will reduce your gains on margin by likely more than halve, the remaining gains will in effect likely be taxed more than double.
Which is an unacceptable drag on this strategy. And also dumb, because there is a myriad of ways to bypass this. It sticks out like a sore thumb in a legal environment where you pay taxes once on net gains only.
Enter Options
tl;dr: Box spreads can give you cheap margin capital. Interest is paid through capital loss.
Please don’t touch this, if you don’t know what you are doing. Other people have thought that “it can’t go tits up” before. But options can potentially be one more useful tool at your disposal (if read up on them until you understand).
Maybe some have heard about box spreads (shout-out to the unanswered question by @Ewian). Basically:
The difference is equivalent to the interest you pay for the period. It should be possible to get it a bit above the risk free rate with liquid options (e.g. options on SPX). If you can wait for your offer to get filled. If you can’t then you will pay something for the privilege.
On IBKR the cash you will need to pay back is fully margined, so you will get margin called before you don’t have any equity left to pay back.
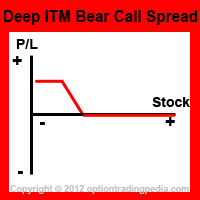
Variation: Deep ITM Bear Call Spread
tl;dr: This is especially interesting if you leverage the underlying.
This nice graphic from optiontradingpedia.com shows the payoff profile:
Since Delta is nearly equal to 1 for each leg, you will just pay the risk free rate plus a bit of spread. Additionally buying and selling the corresponding puts to make a box spread doesn’t add much. They are so far OTM that they are near worthless and mostly push complexity and fees by doubling the amount of options involved.
The cool thing is that, because the underlying is the S&P 500, if there are huge drops, the long call will rise in price stronger than the short call. That is because its strike price is higher. You could sell and re-buy lower for some significant profit. And if it drops catastrophically (far left) you will not have to pay back in full. This goes well with also holding ETFs replicating the S&P 500.
What is also cool is that on IBKR the rules based margin is fixed on the difference between the strikes. Different from Box spreads which additionally considers the cost to close (not nice in a market panic).