The health insurance season is coming and I decided to take a look at it. Let’s start from some formulas. I am going to use following variables, all values are per year:
I = price of the insurance;
F = franchise / deductible;
E = medical expenses, costs of medical services that you are billed on;
C = actual total costs of health insurance and medical services that you are paying.
To simplify things, I didn’t include potential tax deduction or subsidies related to medical costs. And let’s say that we look at more or less standardized obligatory insurance only. The complimentary insurances are very versatile, they have own franchise, so the formulas could be adapted to them as well.
From the financial point of view, the obligatory health insurance in Switzerland works as following (as explained in my Assura app, I hope they know what they are doing). You choose an insurance plan with franchise F that costs I per year. If medical expenses are less than the franchise (E < F), you don’t get anything from the insurance.
E < F: C = I + E (1)
If your medical expenses exceed the franchise (E > F), you pay only 10% of expenses above the franchise, up to 700 CHF.
F < E < E_max: C = I + F + 0.1*(E - F) (2)
Once the expenses have reached the value of E_max, your costs are capped to
E >= E_max: C_max = I + F + 700 CHF (3)
Therefore we can calculate E_max as following:
0.1*(E_max - F) = 700 CHF; E_max = 7000 CHF + F (4)
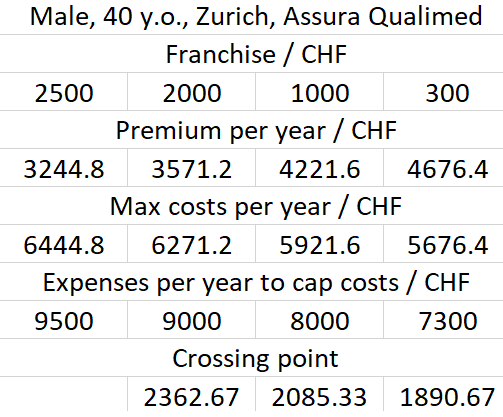
Now let’s look at some examples (data are from comparis.ch):
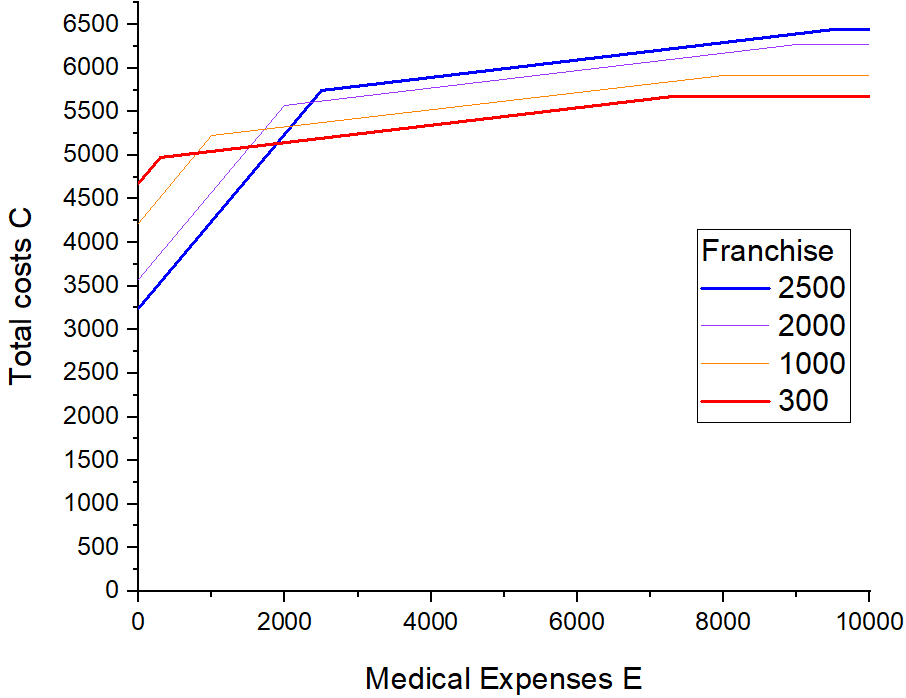
And graphically: what are the total cost C as a function of medical expenses E in these cases.
Here one can see very well what is usually said: the lowest total costs are achieved either with the highest or with the lowest franchise.
Now let’s look at the cross point of total costs for insurances with a higher and a lower franchise, E_x. For the insurance with the higher franchise F0 that costs I0, E_x < F0, therefore
C = I0 + E_x (5)
For an insurance with the lower franchise F1 that costs I1, F1 < E_x < E_max1, therefore
C = I1 + F1 + 0.1*(E_x - F1) (6)
Solving for E_x, we obtain
E_x = F1 + (I1 - I0)/0.9 (7)
If we look at the equation 7, E_x is lowest when F1 + I1/0.9 is lowest. If one looks at the table again and do some more calculations (not shown), then we can see that the decrease of the yearly premium I corresponds very well to 65% of the increase of the franchise F. Therefore the crossing point is moving according to the following relation
ΔE_x ≈ (1-(0.65/0.9))*ΔF = 0.28*ΔF(8)
Therefore the lower the franchise, less expenses are needed to reach the point where this insurance has lower total costs than the insurance with the higher franchise.
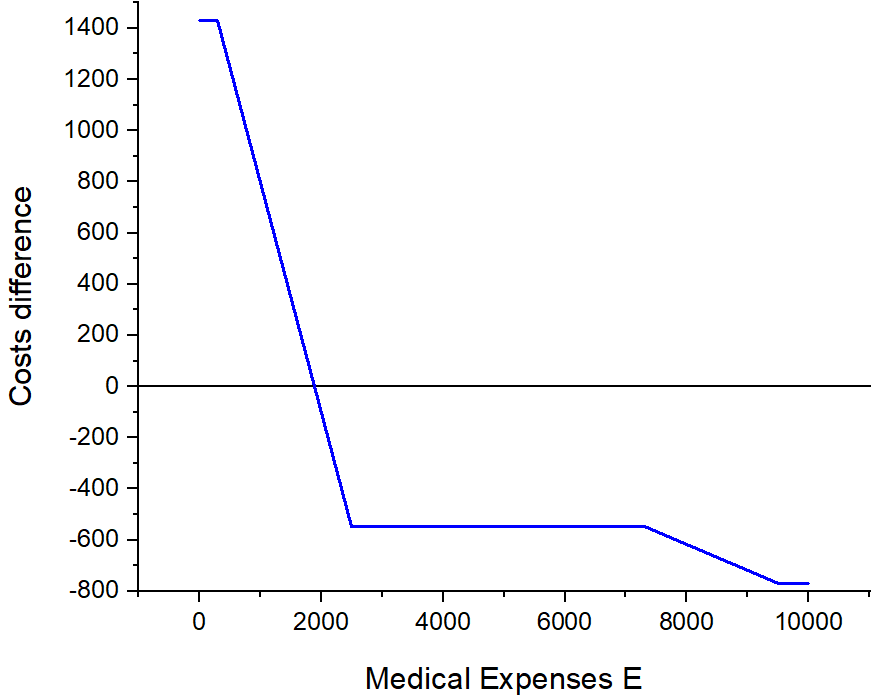
Now let’s look at the costs difference between the insurances with franchise 300 CHF and 2500 CHF.
As you can see, the absolute value of the difference is higher at lower expenses, i.e. when total costs of 2500 CHF insurance is lower. In other words, if you choose 2500 CHF over 300 CHF, you can save up to 1430 CHF or you can “lose” up to 770 CHF if your medical expenses are very high. This asymmetry means that even if there is a 50% probability that from one year to another your medical expenses will be higher or lower than E_x, the insurance with higher franchise still comes cheaper.
For me the message is very clear. If you are not sure about your expenses, take an insurance with the highest franchise. Only if one is certain that the medical expenses will be higher than E_x, for example there is a repeated treatment that costs you more than roughly 2k per year, one should choose the lowest franchise. The rest is a confusion created by medical insurance businesses and can go to hell.
As always I am looking forward to your comments and corrections.